ビッグデータの新しい統計法則の発見

同大学の梅野健 情報学研究科教授、新谷健 同修士課程学生（現・フォルシア社員）が発見。研究成果は、日本物理学会の国際学術誌『Journal of the Physical Society of Japan』速報版にオンライン公開された。

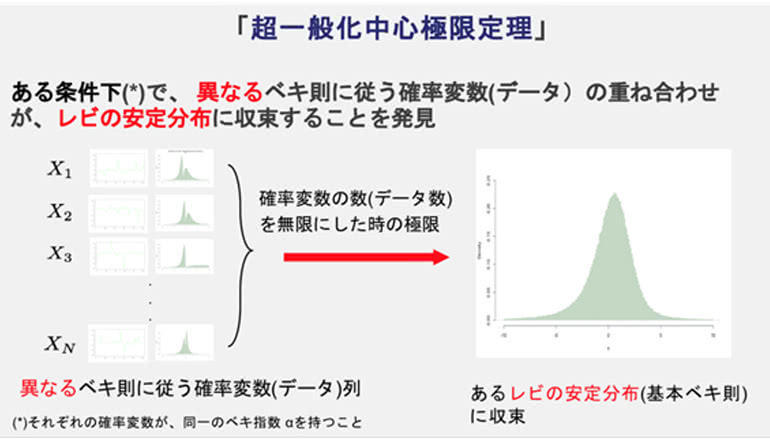
研究では、現実のデータを反映した、従来の統計則である極限定理では捉えることができない、異なるべき分布を個々に持つ独立な確率変数の和という統計モデルを定式化した。その上で、データの数Nを無限にする極限において、「レビの安定分布」というべき則の基本形（基本べき則）に収束するという極限定理を導出した。

べき則とは、確率分布が、規分布（ガウス分布）の様に、変動幅に対して指数関数的にゼロに減衰するのではなく、変動幅に対してべき的にゆっくりゼロに減衰すること。また、レビの安定分布とは、ベき指数α(0<α≦2)と歪度β(-1≦β≦1)の2つの基本パラメータを持つ確率分布であり、独立な確率変数の和は適当な一次変換によって元の分布になるという特徴を持つ。

この極限定理は、統計学の基本法則である中心極限定理をべき則に一般化した一般化中心極限定理をさらに異なるべき則の和の極限に拡張したもの。研究グループによると、「超一般化中心極限定理」と呼ぶことができる。より一般化された状況でも成立する極限定理としての統計学的な意義があるとともに、現実世界の至るところにあらわれるべき則の普遍性を示すビッグデータの特徴を正確に記述する基本統計則としての意義も持つと考えられるという。

今回得られた超一般化中心極限定理を、金融市場の株価変動や為替変動、地震の間隔といった実データに基づくデータ解析に適用し、その極限定理のもつべき則の基本形であるレビ安定分布のパラメータ(α（べき指数）、β（歪度））によって、世界の様々な現象の統計モデル化を行っていく。さらに、金融市場の安定性とこれらのパラメータがどのように関わっているかなどを検証する予定。