バイオ
半世紀にわたる生命現象モデルの理解が前進
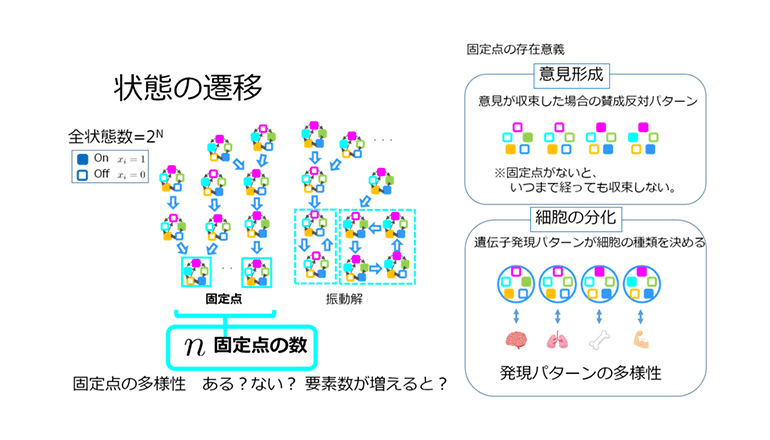
それが提案されたのはずいぶん昔のことであり、近年では社会現象のモデルとしても再注目されている。意見の賛成・反対のように、0か1かで表される要素が相互に作用し合って多彩な力学を生み出すネットワークは、様々な系で数多くみられる。
各要素は周囲の状況に応じて状態を決める性質や性格を有していて、それをブール関数――0か1の入力集合に、0か1の出力を返す――と捉えて生命現象の基礎、遺伝子制御系のモデルとして「ブーリアンネットワーク」が提案された。約50年前から、リンクの向きが定義された有向ネットワークで互いにつながった0か1は、ある初期状態から出発すると、それ以上状態の変わらない「固定点」か、状態が周期的に変わる「振動解」かに落ち着く。系の持つ固定点の数は、細胞種類の多様性や意見収束の実現性と密接に関係し重要である。だがその数はネットワークのつながり方(トポロジー)とブール関数の割り振り方双方に依存するため、広い条件下での理論的記述は困難であったという。
理化学研究所 望月理論生物研究室の森史協力研究員と望月敦史主任研究員の研究チームは、ネットワークを任意のトポロジーに固定し、各要素のブール関数をさまざまな確率分布に従ってランダムに割り振ると仮定した状況で、「確率的に中立なリンクの集合が"Feedback Arc Set"であるならば、固定点数の平均値は1である」という、広い条件下で成立する極めて簡潔な定理を導出した。
ブーリアンネットワークでの表現が妥当なすべての系に適用できる。新しい定理、即ち新たな不変量による理論的手法は、振動解の数やその周期の長さなど固定点数以外の特徴量の解析にも応用できる見込みだという。研究は科学技術振興機構の「生命動態の理解と制御のための基盤技術の創出」の一環で行われた。そしてその成果は、米国の科学雑誌「Physical Review Letters」にも掲載される。
